Statistical Rethinking 제2장 연습문제 풀이

책 홈페이지: https://xcelab.net/rm/statistical-rethinking/

 

2M1 풀이

# Define grid
p_grid = seq(from=0, to=1, length.out=20)

# Prior
prior = rep(1, 20)

# Likelihood
# 2M1 (1)
W = 3
N = 3
## 2M1 (2)
#W = 3
#N = 4
## 2M1 (3)
#W = 5
#N = 7
likelihood = dbinom(x=W, size=N, prob=p_grid)

# Posterior
posterior = likelihood * prior
posterior = posterior / sum(posterior)

# Plot
plot(p_grid, posterior, type="b", xlab="Probability of water", 
     ylab="Posterior probability")

결과

 

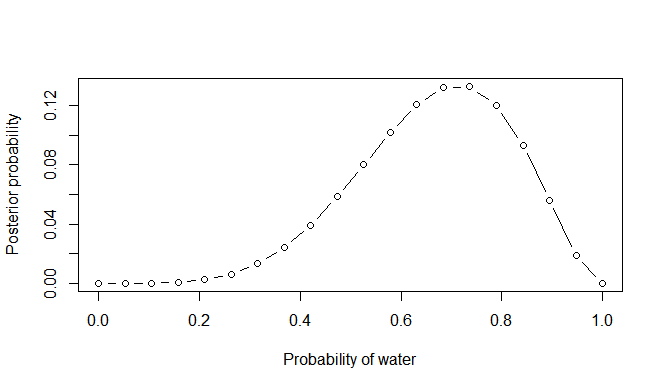
2M2 풀이

2M1의 R script중 prior 부분만 아래와 같이 바꾸면 된다.

# Prior
prior = ifelse(p_grid < 0.5, 0, 1)

결과는 W = 5, N = 7일때만 보여주고 나머지는 생략한다.

 

2M3 풀이

 

2M4 풀이

	Up	Down
BB	B	B
	B	B
BW	B	W
	W	B
WW	W	W
	W	W

Up이 B인 경우 3가지

Up이 B일때 Down이 B인 경우 2가지

답 2/3

 

2M5 풀이

	Up	Down
BB	B	B
	B	B
BW	B	W
	W	B
WW	W	W
	W	W
BB	B	B
	B	B

Up이 B인 경우 5

Up이 B일때 Down이 B인 경우 4

답 4/5

 

2M6 풀이

	Up	Down	likelihood	prior	likelihood * prior	posterior probability
BB	B	B	2	1	2	2/4 = 0.5
	B	B
BW	B	W	1	2	2	2/4 = 0.5
	W	B
WW	W	W	0	3	0	0
	W	W
Sum					4

BW를 뽑는 경우가 BB를 뽑을 경우보다 2배 많고

WW를 뽑는 경우가 BB를 뽑는 경우보다 3배 많다고 했으므로 prior가 각각 1, 2, 3

답은 맨 오른쪽 위에 있는 0.5

 

2M7 풀이

	Up	Down	likelihood	prior	likelihood * prior	posterior probability
BB	B	B	2*3	1	6	6/8 = 0.75
	B	B
BW	B	W	1*2	1	2	2/8 = 0.25
	W	B
WW	W	W	0	1	0	0
	W	W
Sum					8

이 문제의 prior는 모두 1.

BB인 경우는 3을 더 곱해주어야 하는데 BB를 뽑은 후 W를 뽑는 경우의 수는 BW에서 1 그리고 WW에서 2번.

BW인 경우는 WW에서 W를 2번 뽑을수 있으므로 2를 곱해주어야 한다.