Notice
Recent Posts
Recent Comments
Link
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 |
Tags
- 히스토그램
- 우분투
- post hoc test
- 풍백
- categorical variable
- Histogram
- ANOVA
- spss
- 후한서
- 낙랑군
- repeated measures ANOVA
- t test
- R
- 기자
- 지리지
- 고구려
- 패수
- linear regression
- 기자조선
- 한서지리지
- 단군
- 독사방여기요
- 통계
- 태그를 입력해 주세요.
- 선형회귀분석
- 통계학
- 신라
- 창평
- 유주
- 한서
Archives
- Today
- Total
獨斷論
통계기초 정리 1 본문
1. Mean
- Population Mean
$$\mu = \frac {\sum x} {N}$$
- Sample Mean
$$\bar{x} = \frac {\sum x} {n}$$
Median
중간에 있는 값
Mode
가장 많은 frequency를 갖는 값
Skew left

Skew right

2. Standard deviation
- Sample standard deviation
$$s = \sqrt{\frac {\sum (x - \bar{x})^2}{n-1}}$$
- Population standard deviation
$$\sigma = \sqrt{ \frac {\sum (x-\mu)^2}{N}}$$
3. Empirical rule

정규분포 데이터의 95%는 평균의 2$\sigma$ 범위 안에 들어온다.
4. z-score
표준정규분포를 따르는 데이터로 만들수는 있지만 항상 표준정규분포를 따르지는 않는다.
$$z = \frac{x - \bar{x}}{s}$$
여기서
$x=$ 데이터변수
$\bar{x}=$ x의 평균
$s=$ x의 표준편차
5. Five Number
- Minimum: 가장 작은 값을 의미하지만 보통 $Q1 - 1.5 \times IQR$ 로 사용
- First quartile Q1: 25th percentile
- Median: Q2, 50th percentile
- Third quartile Q3: 75th percentile
- Maximum 가장 큰값을 의미하지만 보통 $Q3 + 1.5 \times IQR$
Minimum과 Maximum 밖의 값을 outlier이다.
Interquartile range
$$IQR = Q_3 - Q_1$$
6. Box plot
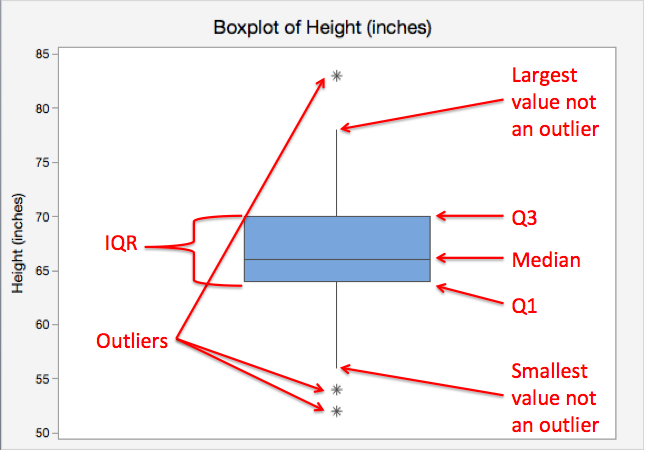
가운데 네모로 된건 Q1에서 Q3의 값들이고 그 중간에 Median이다.
위아래 선으로 연결된것은 최대값과 최소값을 나타내고
별표는 Outlier이다.
7. Pearson's Correlation
$$r_{xy} = \frac {\sum (x_i - \bar{x}) (y_i - \bar{y})} {\sqrt{\sum (x_i - \bar{x})^2} \sqrt{\sum (y_i - \bar{y})^2}}$$
Properties
- $-1 \le r \le 1$
- r이 양수이면 x가 증가할때 y도 증가, r이 음수이면 x가 증가할때 y가 감소
| r의 값 | |
| 0 ~ 0.2 | Very weak |
| 0.2 ~ 0.4 | Weak |
| 0.4 ~ 0.6 | Moderate |
| 0.6 ~ 0.8 | Strong |
| 0.8 ~ 1.0 | Very strong |
Outlier에 민감하게 변화한다.
Comments

