| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- 고구려
- 후한서
- categorical variable
- 한서지리지
- 선형회귀분석
- 풍백
- Histogram
- 유주
- post hoc test
- 독사방여기요
- 기자
- 단군
- ANOVA
- 태그를 입력해 주세요.
- t test
- 우분투
- 신라
- spss
- linear regression
- 지리지
- 패수
- repeated measures ANOVA
- 한서
- 통계
- 히스토그램
- 기자조선
- 창평
- R
- 낙랑군
- 통계학
- Today
- Total
목록과학과 기술/통계이론설명 (31)
獨斷論
 확률이론 정리10. 카이제곱분포(Chi-Square Distribution)
확률이론 정리10. 카이제곱분포(Chi-Square Distribution)
카이제곱분포 감마분포에서 θ=2이고 α=r2이고 이때 r은 양의 정수라고 할때 확률밀도함수 f(x)는 f(x)=1Γ(r/2)2r/2xr/2−1e−x/2 이고 이때 확률변수 X는 자유도가 r인 카이제곱분포를 따른다고 말한다. 주로 χ2(r)로 나타낸다. 평균과 분산 μ=E(X)=r σ2=2r Upper 100αth percentile α를 0과 1 사이의 확률이라고 생각할때(위 감마분포의 α가 아님), 자유도가 r인 카이제곱 분포의 upper 100αth percentile은 $\chi^..
 확률이론 정리9. 감마 분포(Gamma Distribution)
확률이론 정리9. 감마 분포(Gamma Distribution)
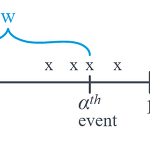
일정한 시간(또는 거리 구간 같은 물리량)에서 사건이 X번 일어날 확률은 포아송분포로 나타낼수 있고 사건이 일어나는 비율 λ는 일정해야만 한다. f(x)=e−λλxx! 포아송분포와 같은 사건에 대하여 첫번째 사건이 일어나는데 걸리는 시간(또는 구간)을 확률변수 W라 하면, 이때 확률변수 W는 지수분포를 따른다. f(w)=1θe−w/θ 여기서 θ=1λ 이제 α번째 사건이 일어나는데 걸리는 시간을 확률변수 W로 나타내면 이 확률변수 W는 다음과 같은 확률분포를 따른다 $$f(w)=\dfrac{1}{(\alpha-1..
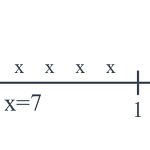 확률이론 정리8. 지수분포(Exponential Distribution)
확률이론 정리8. 지수분포(Exponential Distribution)
X가 포아송 확률변수이고 일정가간동안 은행에 도착하는 손님수라고 가정하자. 이때 λ를 일정기간( 또는 1기간)동안 도착하는 평균 손님수라고 하면 처음으로 손님이 도착하는데 걸리는 시간을 확률변수 W로 나타내면, 첫번째 손님이 도착하는데 걸리는 평균시간, θ는 1/λ와 같다. θ=1λ 이때 첫번째 손님이 도착하는게 걸리는 시간은 지수분포(exponential distribution)를 따른다. 지수분포 X가 지수분포를 따르는 확률변수일때 확률밀도함수는 다음과 같다 f(x)=1θe−x/θ 여기서 θ>0이고 x≥0이다. ..
포아송 분포 X가 포아송 확률변수일때 p.m.f.는 다음과 같다. f(x)=e−λλxx! 여기서 x=0,1,2,⋯이고 λ>0 평균과 분산 E(X)=λ σ2=λ 예제 X가 인쇄된 책 1쪽당 발생할 인쇄오류갯수라고 할때, 이 책에서 임으로 1쪽을 선택할때 적어도 1개 이상의 인쇄오류가 발생할 확률은? λ=3 적어도 한개이상 오류가 발생할 확률은 P(X≥ 1)=1−P(X=0)이므로 $\begin{align} P(X \ge 1) &= 1 - \frac {e^{-3} 3^{0}} {0!} \\ &= 1 - e^{-3} \\..
기하분포(Geometric Distribution) 성공할 확률이 p이고 실패할 확률이 1−p인 시행에 있을때, X를 이 시행을 성공할때까지 수행한 횟수라고 하면 X의 probability mass function은 f(x)=P(X=x)=(1−p)x−1p 여기서 x=1,2,⋯ 이때 X를 기하분포를 따른다고 말한다. 누적분포함수 F(x)=P(X≤x)=1−(1−p)x 평균 μ=E(X)=1p 분산 σ2=1−pp2 예제1 국가평균으로 박사의 비율이 0.2라고 가정하고, 길거리에서 임으로 사람을 선택하여 최종학력을 물어왔을때, 4명을 만나야만 박사학..
 확률이론 정리5. 이항분포(Binomial distribution)
확률이론 정리5. 이항분포(Binomial distribution)
이항확률변수 X의 p.m.f.는 f(x) = \dbinom{n}{x} \, p^x \, (1-p)^{n-x} 이고 아래와 같이 나타내기도 한다. X \sim b(n, p) 이산확률변수 X는 다음조건을 만족하면 이항확률변수가 된다. 실험이 똑같은 방법으로 n번 반복한다. 각각의 n개의 실험은 두개의 결과만 갖는다(성공 또는 실패). 이러한 실험을 Bernoulli trial이라고 한다. n개의 실험은 서로 독립이다. 두개의 결과중 성공할 확률이 p이면 실패할 확률은 1-p이다. 확률변수 X는 n번 실험에서 성공할 횟수이다. 표본크기 n이 모집단의 크기 N과 비슷하다면 Bernoulli trial의 확률 p가 변하므로 이항분포라고 말할수가 없다. 엄밀히 말하면 이는 hypergeometri..
확률변수 X의 적률생성함수 X가 이산확률변수이고 pmf가 f(x)이고 support가 S일때 M(t) = E( e^{tX} ) = \sum_{x \in S} e^{tx} f(x) 를 X의 적률생성함수라고 한다. 이때 t는 -h \lt t \lt h인 h가 존재해야만 한다. 예제 Binomial 확률변수의 적률생성함수 구하기 $\begin{align} M(t) &= E\left(e^{tx} \right)\\ &= \sum_{x=0}^n e^{tx} f(x) \\ &= \sum_{x=0}^n e^{tx} \dbinom{n}{x} p^x (1-p)^{(n-x)} \\ &= \sum_{x=0}^n \dbinom{n}{x} (p e^t )^x (1-p)^{(n-x)} \\ &= \left[ (1-p) ..
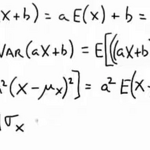 확률이론 정리3. 이산분포(Discrete distribution)
확률이론 정리3. 이산분포(Discrete distribution)
Probability Mass fucntion(p.m.f) 이산확률변수 X에 대하여 이산질량함수(probability mass function) P(X = x) = f(x)는 다음을 만족한다. P(X = x) = f(x) \gt 0 \sum\limits_{x \in S} f(x) = 1 P(X \in A) = \sum\limits_{x \in A} f(x) Cumulative distribution function(CDF) 확률변수 X의 누적분포함수는 다음과 같이 정의된다. F_X (t) = P(X \le t) CDF의 성질들 F_X (t)는 증가하는 함수이다. t의 범위는 -\infty \lt t \lt \infty 0 \le F_X (t) \le 1 확률변수 X..
