獨斷論

SPSS 파일: 변수설명 marketid: Market ID (Nominal) mktsize: Market size (Ordinal) locid: Location ID (Nominal) ageloc: Age of store location (Scale) promo: Promotion ID (Nominal) sales: Units sold (Scale) 문제설명 새로운 상품을 선전하기 위해 광고를 3가지로 준비하였고(promo), 어떤 광고가 가장 효과적인지 알아보기 위하여 10개의 시장의(marketid) 각각 다른 상점의 위치를 정하여(locid) 서로 다른 광고를 하였을때 1달동안 팔린 상품의 양을 조사하였다(sales) 이때 3가지 광고중에 가장 효과적인 광고를 분석하여 보자. 분석방법 Analyz..

# 두 개의 데이터가 있다고 가정 data1

27 Survival analysis 27.1 Overview Survival analysis focuses on describing for a given individual or group of individuals, a defined point of event called the failure (occurrence of a disease, cure from a disease, death, relapse after response to treatment…) that occurs after a period of time called failure time (or follow-up time in cohort/population-based studies) during which individuals are ..

### ### Tutorial of survival analysis ### ## subject time event ## 1 1 3 0 ## 2 2 5 1 ## 3 3 7 1 ## 4 4 2 1 ## 5 5 18 0 ## 6 6 16 1 ## 7 7 2 1 ## 8 8 9 1 ## 9 9 16 1 ## 10 10 5 0 ## ## where: ## ## subject is the individual’s identifier ## time is the time to event (in years)2 ## event is the event status (0 = censored, 1 = event happened) # library(survival) ## Example 1 # Data input survDat = ..

파일명이 "NUL"인 파일이 안 지워질때 해결방법 예를들어 D:\WORK에 NUL이라는 파일이 존재하지만 지워지지 않는다면 COMMAND PROMPT를 관리자로 열고 해당파일이 있는 곳으로 이동한다 D: CD D:\WORK 그리고 아래와 같이 실행하여 NUL을 deletefile.txt로 바꾼다 D:\Work>rename \\.\d:\work\NUL. deletefile.txt 그러면 deletefile.txt은 파일탐색기로 지울수 있다.

카이제곱분포 감마분포에서 $\theta=2$이고 $\alpha= \dfrac{r}{2}$이고 이때 $r$은 양의 정수라고 할때 확률밀도함수 f(x)는 $$f(x)=\dfrac{1}{\Gamma (r/2) 2^{r/2}}x^{r/2-1}e^{-x/2}$$ 이고 이때 확률변수 $X$는 자유도가 $r$인 카이제곱분포를 따른다고 말한다. 주로 $\chi^2 (r)$로 나타낸다. 평균과 분산 $$\mu = E(X) = r$$ $$\sigma^2 = 2r$$ Upper 100$\alpha^{th}$ percentile $\alpha$를 0과 1 사이의 확률이라고 생각할때(위 감마분포의 $\alpha$가 아님), 자유도가 r인 카이제곱 분포의 upper 100$\alpha^{th}$ percentile은 $\chi^..

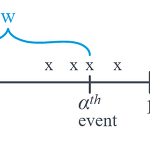
일정한 시간(또는 거리 구간 같은 물리량)에서 사건이 $X$번 일어날 확률은 포아송분포로 나타낼수 있고 사건이 일어나는 비율 $\lambda$는 일정해야만 한다. $$f(x)=\dfrac{e^{-\lambda} \lambda^x}{x!}$$ 포아송분포와 같은 사건에 대하여 첫번째 사건이 일어나는데 걸리는 시간(또는 구간)을 확률변수 $W$라 하면, 이때 확률변수 $W$는 지수분포를 따른다. $$f(w)=\dfrac{1}{\theta} e^{-w/\theta}$$ 여기서 $\theta = \dfrac {1}{\lambda}$ 이제 $\alpha$번째 사건이 일어나는데 걸리는 시간을 확률변수 $W$로 나타내면 이 확률변수 $W$는 다음과 같은 확률분포를 따른다 $$f(w)=\dfrac{1}{(\alpha-1..

$X$가 포아송 확률변수이고 일정가간동안 은행에 도착하는 손님수라고 가정하자. 이때 $\lambda$를 일정기간( 또는 1기간)동안 도착하는 평균 손님수라고 하면 처음으로 손님이 도착하는데 걸리는 시간을 확률변수 $W$로 나타내면, 첫번째 손님이 도착하는데 걸리는 평균시간, $\theta$는 $1 / \lambda$와 같다. $$\theta = \frac {1}{\lambda}$$ 이때 첫번째 손님이 도착하는게 걸리는 시간은 지수분포(exponential distribution)를 따른다. 지수분포 $X$가 지수분포를 따르는 확률변수일때 확률밀도함수는 다음과 같다 $$f(x) = \frac {1}{\theta} e^{-x / \theta}$$ 여기서 $\theta \gt 0$이고 $x \ge 0$이다. ..