| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 |
- 고구려
- 히스토그램
- 풍백
- linear regression
- 통계학
- 한서지리지
- repeated measures ANOVA
- 태그를 입력해 주세요.
- 지리지
- 통계
- categorical variable
- 후한서
- 우분투
- 기자조선
- 한서
- R
- 낙랑군
- ANOVA
- t test
- post hoc test
- 기자
- spss
- Histogram
- 독사방여기요
- 선형회귀분석
- 창평
- 유주
- 단군
- 신라
- 패수
- Today
- Total
獨斷論
SAS 문법 - 12: 범주형변수 proc freq 수행하기 본문
SAS 라이브러리 파일을 받아서 원하는 디렉토리에 저장한다.
일원빈도표(one-way frequency table)
libname icdb 'd:\tmp';
proc freq data=icdb.back;
tables sex race;
run;위 SAS 코드를 실행하면 sex와 race 두 범주형변수에 대하여 일원빈도표(일원도수표)를 만든다. tables sex와 race를 넣지 않으면 모든변수에 대하여 도수표를 만들게 된다.

범주형변수의 각 수준(level)에 대하여 빈도표를 만들려면 proc sort를 수행한 후에 proc freq 안에 by 문장을 넣어서 SAS 코드를 수행하면 된다.
proc sort data=icdb.back out=s_back;
by sex;
run;
proc freq data=s_back;
tables ed_level;
by sex;
run;proc sort에서 성별에따라 정렬을 한 후에 s_back이라는 데이터집합에 넣었다.
proc freq에서 정렬된 s_back을 이용하여 성별에 따라 ed_level의 빈도표를 만들었다.
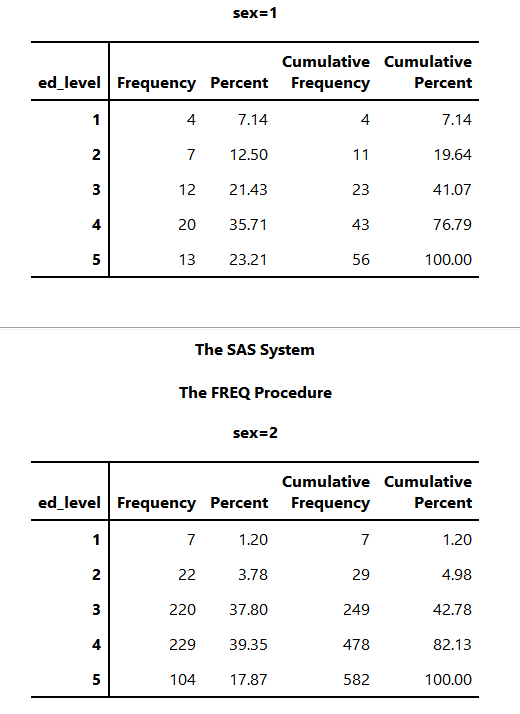
변수값에 결측값이 있는 경우에는 결측값을 빼고 계산한다. 만약 결측값이 몇개인지 알아보고자 한다면 missing이나 missprint 옵션을 이용한다.
DATA mydat;
INPUT subj 1-4 gender 6 height 8-9 weight 11-13;
DATALINES;
1024 1 65 125
1167 1 68 140
1168 . 68 190
1201 2 72 190
1302 1 63 115
;
RUN;
proc freq data=mydat;
title 'No option to tables statement';
tables gender;
run;
proc freq data=mydat;
title 'missing option to tables statement';
tables gender /missing;
run;
proc freq data=mydat;
title 'missprint option to tables statement';
tables gender /missprint;
run;결과는 아래와 같다.
옵션 없음

missing 옵션 사용

missprint옵션 사용

이원빈도표(Two-way frequency table)
2개의 변수를 가로 세로 변수로 놓고 빈도표를 만들어보자. 성별에 따른 교육수준을 표로 만들면
libname icdb 'd:\tmp\';
proc freq data=icdb.back;
tables ed_level * sex;
run;
- 성별이 남자(sex = 1)이고 교육수준이 1인 사람은 4명이다.
- 전체 638명중 4명은 62.7%($4 / 638 \times 100 = 0.626$)에 해당한다. 위 표에서는 0.63%로 나와있다.
- 교육수준이 1이고 성별이 남자(sex = 1)인 사람은 여자를 포함한 교육수준이 1인 사람의 36.36%에 해당한다($4/11 \times 100 = 36.36$).
- 교육수준이 1인 남자는 전체 남자의 7.14%에 해당한다($4/56 \times 100 = 7.14$).
위 빈도표는 약간 지저분 하므로 1-4를 선택하여 출력할수가 있다.
- NOFREQ : 표에서 빈도를 없앤다 (위에서 4명에 해당).
- NOPERCENT 전체 %를 없앤다 (위 표의 0.63).
- NOROW row percent를 없앤다 (위 표의 36.36).
- NOCOL column percent를 없앤다(위 표의 7.14).
따라서 빈도만 출력하고 싶다면
proc freq data=icdb.back;
tables ed_level * sex / nocol norow nopercent;
run;
또한 각 cell마다 statistic을 추가할수 있다.
- expected : null hypothesis of independence에 의하여 각 cell 빈도의 기대값을 출력
- cellchi2 : chi squared statistic을 출력
$$\textrm{cellchi2} = \frac { (\textrm{frequency} - \textrm{expected})^2 } {\textrm{expected}}$$
proc freq data=icdb.back;
tables ed_level * sex / expected cellchi2 nocol norow nopercent;
run;

이원빈도표가 너무 지저분하다고 생각되면 이를 아래로 늘리면 쉽게 볼수있다.
list나 crosslist를 사용하는데 list의 결과에는 row percent, column percent, percent등이 포함되지 않는다.
proc freq data=icdb.back;
tables sex * ed_level / crosslist;
* tables ed_level * sex / crosslist;
run;
list 옵션을 사용한 경우
proc freq data=icdb.back;
tables ed_level * sex / list;
run;
데이터로 저장하기
out 옵션을 이용하여 proc freq의 결과를 데이터로 만들수도 있다.
proc freq data=icdb.back;
tables sex * race /out=sexfreq noprint;
run;
proc print data=sexfreq;
run;
sexfreq라는 데이터를 다른 분석에 이용할수 있도록 일렬로 데이터형태를 만들어 저장되었다. noprint옵션을 제거하고 위 SAS코드를 실행하면 어떻게 다른지 알수가 있다.
위 출력결과에서 sex와 race가 0인것들은 모두 제거되었는데 이를 포함시키려면 sparse 옵션을 사용한다.
proc freq data=icdb.back;
tables sex * race /out=sexfreq noprint sparse;
run;
proc print data=sexfreq;
run;



