| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- 한서지리지
- 낙랑군
- 고구려
- 태그를 입력해 주세요.
- linear regression
- 패수
- 단군
- 통계
- 창평
- spss
- 우분투
- 풍백
- 한서
- 후한서
- R
- ANOVA
- 유주
- 신라
- 기자조선
- 독사방여기요
- repeated measures ANOVA
- t test
- categorical variable
- 선형회귀분석
- 기자
- post hoc test
- 지리지
- Histogram
- 히스토그램
- 통계학
- Today
- Total
獨斷論
SPSS 사용법 - MANOVA 본문
SPSS 사용법 - MANOVA(Multivariate ANOVA)
다변량분산분석, Multivariate ANOVA, multivariate analysis of variance,
MANOVA는 multivariate analysis of variance의 준말이며 ANOVA와는 달리 종속변수가 2개 이상인 모델을 말한다. MANOVA는 종속변수끼리 서로 약한 상관관계가 있을때 사용하는 모델이며 강한 상관관계가 있다면 multicollinearity(다중공선성)의 위험성이 있어 해석하는데 문제가 있다. 만약 종속변수가 많지만 종속변수가 서로 독립이라면 MANOVA를 이용할 필요는 없고 종속변수의 갯수만큼 ANOVA를 수행하면 도니다.
MANOVA의 가정
- 각각의 observation 또는 subject가 독립
- multivariate normality
- homogeneity - 모든 group에서 종속변수의 분산과 공분산이 같이야 한다.
MANOVA는 multivariate normality와 homogeneity가 성립하지 않더라도 만약 그룹의 샘플크기가 같다면 결과를 신뢰할 수 있다(가장 큰 그룹의 sample size N이 가장 작은 그룹의 N의 1.5배보다 크면 안된다).
독립변수가 1개인 MANOVA
우선 기본적으로 독립변수가 1개 즉 factor가 1개인 MANOVA를 수행해보기로 하자. 아래 첨부파일을 받아서 SPSS에서 불러들인다.
첨부파일: manova.csv
manova.csv
첨부파일은 학생들의 성적을 조사한 것인데 변수는 아래와 같다.
- gender - 각 학생의 성별(0 = 남자, 1 = 여자)이다.
- faedRevis - 아버지의 교육수준을 나타낸 것이다.
- grades - 학생의 고등학교 성적을 나타낸다.
- mathach - 수학과목의 학업성취도이다.
- visual - Visualization 시험 결과이다.
SPSS의 아랫부분에 "Variable View" 탭을 클릭하여 변수의 성질들을 정의해보자.
- gender - Measure를 Nominal로 지정한다.
- grades - Meausre를 Ordinal로 지정한다.
- faedRevis - Measure를 Ordinal로 지정한다.
Correlation Ceofficients 보기
MANOVA는 종속변수에 상관관계가 있을때 사용하는 것이므로 종속변수에 correlation coefficients가 얼마나 큰지 알아보자.
"Analyze >> Correlate >> Bivariate.."를 클릭하자.
위와같이 correlation coefficients를 알아볼 변수 grades, mathach, visual을 지정한다. 이 변수는 MANOVA에서 종속변수로 사용될 것이다.
아래는 위와 같이 실행하여 본 correlation coefficients의 결과이다.
Significant한 correlation coefficients중에 가장 큰 것은 0.504이다. 만약 correlation coefficients가 0.6보다 크다면 multicollinearity의 문제가 생기므로 그대로 MANOVA를 사용하기보다는 변수를 선형조합을 이용하여 하나의 변수로 만들어 사용한다던지 아니면 변수를 삭제하던지 해야한다.
MANOVA 수행
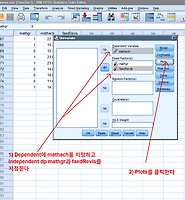
"Analyze >> General Linear Model >> Multivariate..."를 클릭한다.
MANOVA이므로 종속변수가 3개이고 독립변수가 1개이다. 종속변수로는 grades, mathach, visual을 지정하고 독립변수(fixed factor)로는 faedRevis를 지정하였다.
Options를 클릭하여 Multivariate Options라는 대화창이 나타나면 Display의 Descriptive statistics, Estimate of effect size, Parameter estimates, Homogeneity tests의 체크박스를 클릭한다.
Continue를 클릭하고 OK를 클릭하면 아래와 같은 결과를 얻을 수 있다.
가장 큰 그룹의 N = 38이 가장 작은 그룹의 N = 16에 1.5배보다 작아야 가장 좋은 결과를 얻을수 있지만 이 경우에는 그렇지 못하다. 이제 Box's Test의 결과를 보자.
Box's test는 그룹간 covariance의 homogeneity를 테스트하는 것이다. 이 방법은 변수값의 분포가 정규분포이냐에따라 영향을 받으므로 정확하지 않을 수 있다. 그리고 그룹사이의 N이 크게 다르지 않다면 Box test의 결과를 볼 필요는 없다. 본 예제에서는 가장 큰 그룹의 N=38이 가장 작은그룹의 N=16의 2배가 넘으므로 Box test의 결과를 무시하면 안된다.
p-value = 0.147이므로 그룹간에 covariance가 크게 다르지 않음을 알수 있다. 즉, faedRevis의 3그룹 사이의 종속변수의 covariance가 크게 다르지 않다는 것이다. 이는 MANOVA가정을 어기지 않으므로 Wilk's lambda같은 multivariate tests들을 보는 것이 적절하다.
Wilk's lambda의 p-value가 0.008이므로 통계적으로 의미가 있으며 이는 아버지의 교육정도(faedRevis)가 visual test와 수학의 학업성취도(mathach)와 고등학교 성적(grades)에 영향을 미침을 알수있다.
만약 Box's test에서 homogeneity를 위반했다면 univariate ANOVA를 보는 것도 한 방법이겠으나 또한 Pillai's trace를 보는 것도 좋은 방법중의 하나이다(단 Pillai trace는 그룹간의 N이 비슷한 경우에만 가능하며 본 예제에서는 해당되지 않는다).
Levene's test를 보면 mathach의 p-value가 0.049이므로 통계적으로 의미가 있으며 이는 mathach의 분산은 homogeneity의 가정을 위반한다. 따라서 mathach을 transform하여 homogeneity를 따르도록 하여 분석을 다시 수행할 수도 있고, Box's test에서 homogeneity를 위반하지 않는다고 나왔으므로 계속 분석을 수행할수도 있으나 세심한 주의가 필요하다.
위 결과는 univariate ANOVA 결과이다. Homogeneity test의 결과가 가정에 위배되었을때 사용할수도 있다.
어떤 학자는 위 결과를 사용하지 말아야 한다고 주장하기도 한다.
여기서 grades와 mathach가 통계적으로 의미있게 나왔으므로 post hoc multiple comparison을 수행하여 어떤 변수가 가장 많은 영향을 미쳤는지 파악해 봐야만 한다.
위 표에서 Parameter 열에 보이는 [faedRevis=1]은 faedRevis = 1인 그룹과 다른 두 그룹사이의 차이이다. 마찬가지로 [faedRevis = 2]는 faedRevis = 2인 그룹과 다른 두 그룹 사이의 차이이다. faedRevis = 3인 경우는 정보가 중복되므로 생략되었고 여기서는 그냥 0으로 표시하였다.
grades에 대한 [faedRevis = 1]과 mathach에 대한 [faedRevis = 1]의 p-value가 각각 0.006과 0.000이므로 faedRevis가 1인 그룹은 아빠의 교육정도가 학생의 고등학교성적(grades)과 수학학업성취도(mathach)에 크게 영향을 미쳤음을 보여준다.
그러나 [faedRevis = 2]인 그룹은 아버지의 학력이 grades(p = 0.061)에는 어느정도 영향을 미쳤으나 mathach(p = 0.336)에는 크게 영향을 미치지 못하였음을 알수 있다.
visual test의 결과는 아버지의 학력이 어떤 그룹에서도 영향을 미치지 못하였음을 보여준다.