| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- Histogram
- 신라
- linear regression
- 선형회귀분석
- 단군
- 히스토그램
- 지리지
- 기자
- 유주
- 통계
- 고구려
- 후한서
- 풍백
- 통계학
- 한서
- 독사방여기요
- ANOVA
- 태그를 입력해 주세요.
- categorical variable
- spss
- t test
- repeated measures ANOVA
- 우분투
- 낙랑군
- 창평
- R
- post hoc test
- 기자조선
- 한서지리지
- 패수
- Today
- Total
獨斷論
SPSS 사용법 - Multiple Linear Regression 본문
SPSS 사용법 - Multiple Linear Regression (다중회귀분석)
Dependent variable(종속변수)가 하나이고 independent variable(독립변수)가 여러개인 linear regression(회귀분석)을 multiple linear regression(다중회귀분석)이라고 한다. 아래와 같은 식을 사용한다.
y = b0 + b1*x1 + b2*x2 + ... + bk * xk
이를 수행하기 위하여 아래 첨부된 파일을 다운받아 SPSS에서 연다. SPSS파일이 아니라 쉼표로 변수를 나눈 파일이므로 적절한 방법으로 열어아 한다.
첩부파일: FoetalWeight.csv
FoetalWeight.csv
이 파일을 제대로 연다면 아래와 같이 나타날 것이다.
모든 변수는 Numeric과 Scale로 지정해 주어야 한다.
위 데이터의 각 변수에 대해서 잠깐 알아보면 다음과 같다.
- 한 병원에서 414명의 산모를 대상으로 초음파검사로 측정한 값이다.
- MW: 엄마의 몸무게
- MH: 엄마의 키
- GA: 임신기간(측정단위 주週)
- DBMB: 출산과 측정값과의 차이 (측정단위 일日)
- BPD: 체강벽의 직경(biparietal diameter)
- CP: 머리 둘레(cephalic perimeter)
- AP: 복부둘레(abnominal perimeter)
- FL: 넓적다리 길이(femur length)
- FTW: 태어났을때 몸무게
- FTL: 태어났을때 키
- CPB: 태어났을때 머리둘레
본 예제에서는 신생아의 몸무게(FTW)를 임신기간중 초음파로 검사한 아기의 체강벽직경(BPD)와 머리둘레(CP)와 복부둘레(AP)와 엄마의 몸무게(MW)로 linear regression해보기로 한다. 즉,
FTW = b0 + b1*AP + b2*BPD + b3*CP + b4*MW
의 식을 사용한다.
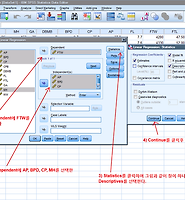
SPSS에서 Multiple linear regression을 수행하기 위해서는 "Analyze >> Regression >> LInear"를 클릭한다.
위의 순서대로 실행하면 아래와 같은 결과를 얻을 수 있다.
Descriptive를 선택하면 위와 같은 correlation을 보여준다. 표로부터 FTW과 correlation이 가장 큰것은 AP(초음파로 찍은 태아의 복부 둘레)이고 가장 correlation이 작은 것은 MW(엄마의 몸무게)임을 알 수 있다.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||||||||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||
FTW = -4936.2 + 120.4AP + 285.3BPD + 35.0CP + 5.5MW
과제물
독립변수로 MW를 제거하고 MH를 넣어 multiple linear regression을 실행한 후에 coefficient 결과에서 significance값이 어떻게 달라지는가? 그리고 이는 무엇을 의미하는가?