Notice
Recent Posts
Recent Comments
Link
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 |
Tags
- 통계
- 패수
- 유주
- 독사방여기요
- Histogram
- 기자
- 히스토그램
- 기자조선
- 한서
- post hoc test
- 지리지
- 단군
- 창평
- ANOVA
- 낙랑군
- t test
- 고구려
- 한서지리지
- 풍백
- 우분투
- 신라
- categorical variable
- 태그를 입력해 주세요.
- 통계학
- repeated measures ANOVA
- R
- spss
- 선형회귀분석
- linear regression
- 후한서
Archives
- Today
- Total
獨斷論
Statistical Rethinking 제4장 연습문제 풀이 본문
4M1 풀이
rm(list = ls())
library(rethinking)
# 4M1
N = 1e4
mu = rnorm(N, 0, 10)
sigma = rexp(N, 1)
y = rnorm(N, mu, sigma)
dens(y)
4M2 풀이
# 4M2
flist =
alist(
y ~ dnorm(mu, sigma),
mu ~ dnorm(0, 10)
sigma ~ dexp(1)
)
4M3 풀이
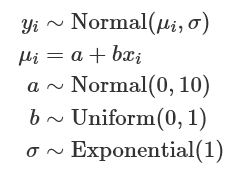
4M4~6 풀이
생략
4M7 풀이
# 4M7
rm(list = ls())
library(rethinking)
data(Howell1)
d = Howell1
d2 = Howell1[d$age >= 18,]
xbar = mean(d2$weight)
flist =
alist(
height ~ dnorm(mu, sigma),
mu <- a + b*(weight - xbar),
a ~ dnorm(178, 20),
b ~ dlnorm(0, 1),
sigma ~ dunif(0, 50)
)
m43 = quap(flist, data=d2)
round(vcov(m43), 3)
weight.seq = seq(from=25, to=70, by=1)
mu = link(m43, data = data.frame(weight=weight.seq))
mu.mean = apply(mu, 2, mean)
mu.PI = apply(mu, 2, PI, prob=0.89)
height.sim = sim(m43, data = list(weight=weight.seq))
height.PI = apply(height.sim, 2, PI, prob=0.89)
windows()
plot(height ~ weight, data=d2, col = col.alpha(rangi2, 0.8))
lines(weight.seq, mu.mean)
shade(mu.PI, weight.seq)
shade(height.PI, weight.seq)
mtext("Centered")위 스크립트는 xbar로 centering하여 선형회귀한 결과이고 covariance는 다음과 같다.
a b sigma
a 0.073 0.000 0.000
b 0.000 0.002 0.000
sigma 0.000 0.000 0.037xbar를 제거한 un-centered로 선형회귀모델을 작성하려면 mu <- a + b*(weight - xbar)에서 xbar만 제거해주면 되고 나머지는 동일하다. covariance결과는 다음과 같다.
a b sigma
a 3.602 -0.078 0.009
b -0.078 0.002 0.000
sigma 0.009 0.000 0.037
4H1 풀이
# 4H1
rm(list = ls())
library(rethinking)
data(Howell1)
d = Howell1
d2 = Howell1[d$age >= 18,]
xbar = mean(d2$weight)
flist =
alist(
height ~ dnorm(mu, sigma),
mu <- a + b*(weight - xbar),
a ~ dnorm(178, 20),
b ~ dlnorm(0, 1),
sigma ~ dunif(0, 50)
)
m43 = quap(flist, data=d2)
weight.dat = data.frame(weight = c(46.95, 43.72, 64.78, 32.59, 54.63))
height.sim = sim(m43, data = weight.dat)
height.expected = apply(height.sim, 2, mean)
height.PI = apply(height.sim, 2, PI, prob=0.89)
weight.dat$expected = height.expected
weight.dat$L89 = height.PI[1,]
weight.dat$U89 = height.PI[2,]
round(weight.dat, 2)
4H2 풀이
# 4H2
rm(list = ls())
library(rethinking)
data(Howell1)
d = Howell1
d2 = Howell1[d$age < 18,]
xbar = mean(d2$weight)
flist =
alist(
height ~ dnorm(mu, sigma),
mu <- a + b*(weight - xbar),
a ~ dnorm(110, 90),
b ~ dlnorm(0, 1),
sigma ~ dunif(0, 50)
)
m43 = quap(flist, data=d2)
weight.seq = seq(from=1, to=50, length.out=100)
mu = link(m43, data = data.frame(weight=weight.seq))
mu.mean = apply(mu, 2, mean)
mu.PI = apply(mu, 2, PI, prob=0.89)
height.sim = sim(m43, data = list(weight=weight.seq))
height.PI = apply(height.sim, 2, PI, prob=0.89)
plot(height ~ weight, data=d2, col = col.alpha(rangi2, 0.9), ylim=c(40, 190))
lines(weight.seq, mu.mean)
shade(mu.PI, weight.seq)
shade(height.PI, weight.seq)
4H3 풀이
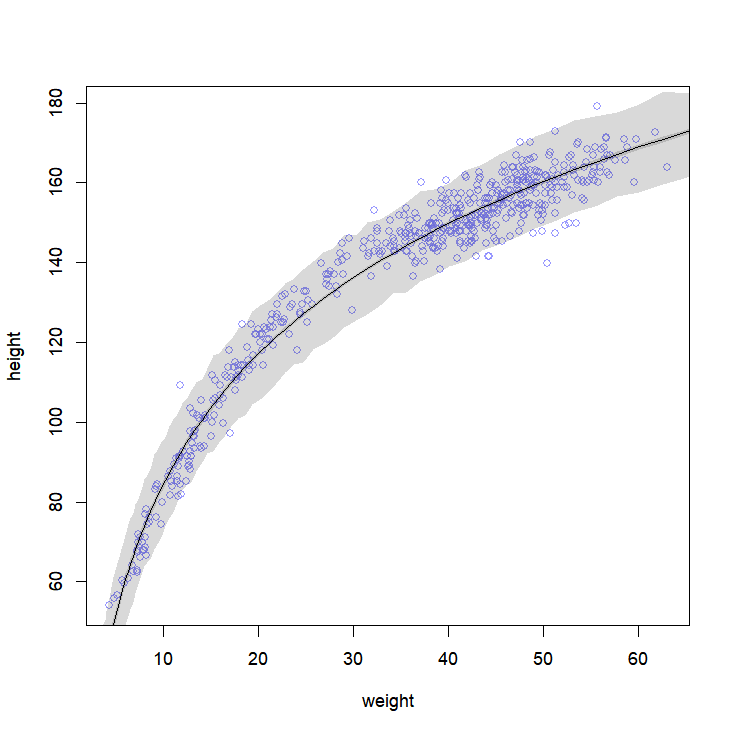
(a) weight 변수를 log_e로 변환하여 선형회귀분석한다.
# 4H3
rm(list = ls())
library(rethinking)
data(Howell1)
d = Howell1
d$log_weight = log(d$weight)
flist =
alist(
height ~ dnorm(mu, sigma),
mu <- a + b*log_weight,
a ~ dnorm(100, 100),
b ~ dlnorm(0, 1),
sigma ~ dunif(0, 50)
)
m43 = quap(flist, data=d)
summary(m43)결과는 대략 이정도 나온다.
> summary(m43)
mean sd 5.5% 94.5%
a -23.74 1.34 -25.88 -21.61
b 47.06 0.38 46.45 47.67
sigma 5.13 0.16 4.89 5.38(b)
log_weight.seq = seq(from=0.5, to=4.5, length.out=100)
mu = link(m43, data = data.frame(log_weight=log_weight.seq))
mu.mean = apply(mu, 2, mean)
mu.PI = apply(mu, 2, PI, prob=0.97)
height.sim = sim(m43, data = list(log_weight=log_weight.seq))
height.PI = apply(height.sim, 2, PI, prob=0.97)
windows()
plot(height ~ weight, data=d, col = col.alpha(rangi2, 0.8))
lines(exp(log_weight.seq), mu.mean)
shade(mu.PI, exp(log_weight.seq))
shade(height.PI, exp(log_weight.seq))weight변수를 log_e를 취했으므로 그래프를 그릴때는 exponential을 취하여 원래대로 돌려놓고 그려야한다.
Comments


