확률이론 정리9. 감마 분포(Gamma Distribution)

일정한 시간(또는 거리 구간 같은 물리량)에서 사건이 $X$번 일어날 확률은 포아송분포로 나타낼수 있고 사건이 일어나는 비율 $\lambda$는 일정해야만 한다.

$$f(x)=\dfrac{e^{-\lambda} \lambda^x}{x!}$$

포아송분포와 같은 사건에 대하여 첫번째 사건이 일어나는데 걸리는 시간(또는 구간)을 확률변수 $W$라 하면, 이때 확률변수 $W$는 지수분포를 따른다.

$$f(w)=\dfrac{1}{\theta} e^{-w/\theta}$$

여기서 $\theta = \dfrac {1}{\lambda}$

 

이제 $\alpha$번째 사건이 일어나는데 걸리는 시간을 확률변수 $W$로 나타내면

이 확률변수 $W$는 다음과 같은 확률분포를 따른다

$$f(w)=\dfrac{1}{(\alpha-1)! \, \theta^\alpha} \, e^{-w/\theta} \, w^{\alpha-1}$$

 

$\theta$는 첫번째 사건이 일어나는데 걸리는 평균시간이고 $\alpha$는 목적하는 사건이 몇번째 일어나는지 나타낸다. . 따라서 $\alpha$가 고정되어있을때 $\theta$가 증가할수록 확률분포는 오른쪽으로 이동하게 된다. 아래 그림에서 3번째 사건을 기다리는데 걸리는 시간는 첫번째 사건이 일어나는데 걸리는 시간이 증가할수록 분포가 오른쪽으로 이동하게 된다.

$\theta$가 고정되어 있고 $\alpha$가 증가하여도 역시 확률분포는 오른쪽으로 이동하게 된다. 아래 그림에서 첫번째 사건이 일어나는데 걸리는 시간이 고정되어 있을때($\theta=3$) 2번째 사건이 일어나는데 걸리는 시간의 분포($\alpha=2$)는 3번째 사건이 일어나는데 걸리는 시간의 분포($\alpha=3$)보다 왼쪽에 위치하게 된다.

 

감마분포

감마분포를 일반적으로 나타내면 다음과 같다.

$$f(x)=\dfrac{1}{\Gamma(\alpha) \, \theta^\alpha} x^{\alpha-1} \, e^{-x/\theta}$$

 

여기서 $\alpha$는 더이상 자연수일 필요는 없고

$\theta \gt 0$

$\alpha \gt 0$

$x \gt 0$

이다.

$\Gamma(\alpha)$는 감마함수라고 부르고

$$\Gamma(t)=\int_0^\infty y^{t-1} e^{-y} dy$$

이며 t가 자연수일때는

$$\Gamma(n)=(n-1)!$$

이 된다.

 

$\alpha=1$이면 감마분포는 지수분포와 같다.

 

평균과 분산

$$\mu = E(X) = \alpha \, \theta$$

$$\sigma^2 = Var(X) = \alpha \, \theta^2$$

 

예제

우주선에 2개의 연료펌프를 장착하고자 하는데 1개는 주요펌프로 쓰이고 다른 1개는 보조펌프로 쓰이는데 첫번째 주요펌프가 고장이 났을때 2번째 보조펌프가 작동되도록 하였다. 우주선이 목적을 달성하기 위해서는 50시간동안 고장이 나지 않고 작동을 해야한다. 그리고 펌프가 고장이 나지 않고 작동하는 평균시간은 100시간이다. 이때 우주선이 50시간의 목적을 달성하지 못하고 펌프가 고장날 확률은 얼마인가?

 

1번째 펌프가 고장이 나고 2번째 펌프가 작동을 한 후에 2번째 펌프도 고장이 나는 시간이 50시간보다 작을 확률을 구하면 된다. $\alpha=2$인 감마분포이고 첫번째 고장(사건)이 일어나는 평균시간은 100시간으로 주어졌으므로 $\theta=100$이다.

따라서 확률밀도함수는

$\begin{align} f(x) &=\dfrac{1}{\Gamma(\alpha) \, \theta^\alpha} x^{\alpha-1} \, e^{-x/\theta} \\ &= \dfrac{1}{100^2 \Gamma(2)}e^{-x/100} x^{2-1} \\ &=\dfrac{1}{10000}xe^{-x/100} \end{align}$

이 되고 50시간 이내에 우주선이 고장이 날 확률은

$\begin{align}  P(X<50)=\int^{50}_0 \dfrac{1}{10000}xe^{-x/100} dy   \end{align}$

가 된다. 부분적분을 이용하면

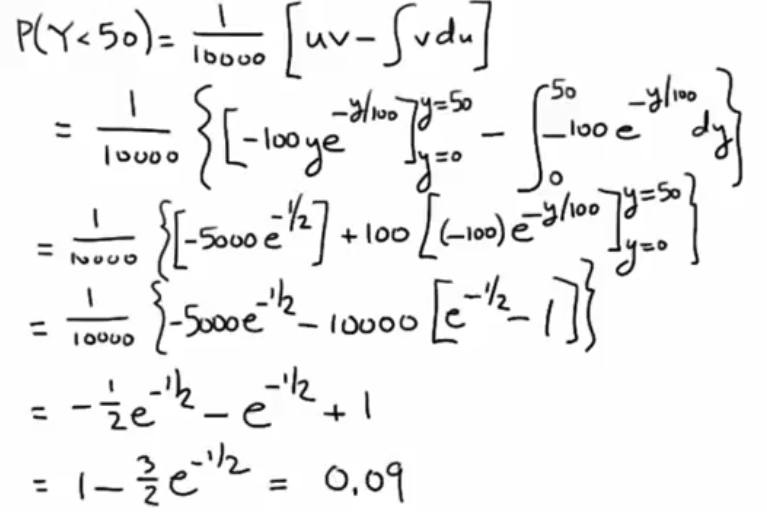
R을 이용하면

> alpha = 2
> theta = 100
> x = 50
> pgamma(q = x, shape = alpha, scale = theta)
[1] 0.09020401

R에서 감마분포를 나타낼때 shape이 $\alpha$이고 scale이 $\theta$가 된다.